第一节 导言

逻辑学是一门基础学科，肇始于古希腊的亚里士多德，而且古印度和中国先秦时期也有类似思想和实践出现；数理逻辑的思想则始于17世纪后半叶。“数理逻辑不外是形式逻辑的精确而又完满的塑述，它有两个很不同的方面。一方面，它是不研究数、函数、几何图形等等，而只是研究类、关系、符号的组合等等的一门科学。另一方面，它又是先于所有其他科学的一门科学，包括作为一切科学的基础的概念和原则。正是在第二种意义下，数理逻辑曾首先由莱布尼茨……所构思。”[※注]莱布尼茨(G.W.Leibniz,1646—1716年)雄心勃勃的逻辑数学化理想由“普遍语言”和“理性演算”两个部分组成。数理逻辑在19世纪中后期诞生，由布尔(G.Boole,1815—1864年)、皮尔士(C.S.Peirce,1839—1914年)和弗雷格(G.Frege,1848—1925年)等人的著作发展起来，沿着这两个部分形成了两个传统，即“数理逻辑传统”和“逻辑代数传统”[※注]，也分别称为“弗雷格—皮亚诺—罗素传统”和“布尔—施罗德—皮尔士传统”，一般统称为符号逻辑、数理逻辑或经典逻辑。在1928—1938年这十年间，数理逻辑的大部分轮廓已经确定，达到发展的“黄金时期”[※注]。1936年，符号逻辑学会(Association for Symbolic Logic)创刊《符号逻辑杂志》(The Journal ofSymbolic Logic)；这是最主要的现代逻辑刊物，第一卷第四期发表了之前所有的符号逻辑文献目录。1977年，第一部逻辑手册《数理逻辑手册》出版，涵盖了符号逻辑(数理逻辑、经典逻辑)作为数学一个部门所包含的公理集合论、证明论、递归论和模型论四个分支的发展成果[※注]，逻辑演算是其基础。

20世纪早期，现代模态逻辑、直觉主义逻辑、多值逻辑等非经典逻辑也出现并发展起来。模态逻辑是关于必然和可能的逻辑，经过句法阶段(1918—1959年)、经典阶段(1959—1972年)，在20世纪70年代达到“黄金时期”，完全性理论、对应理论和对偶理论三大支柱理论在进入现代时期(1972年)[※注]前后相继建立起来。直觉主义逻辑既可以被视为数学中一种哲学的、基础性的主张，也可以被视为数理逻辑内部的一个技术分支；多值逻辑大致开始于1920年前后，第一个已知的公理系统在1931年发表，代数方法在这一族逻辑中的使用特别自然，能够使人们更好地理解多值性问题。[※注]逻辑支撑哲学，哲学哺育逻辑，二者结合便是哲学逻辑。哲学逻辑是运用逻辑方法对哲学概念进行分析而建立的逻辑理论，在20世纪70年代形成了分支数量庞大的领域，为此，符号逻辑学会在1972年创刊《哲学逻辑杂志》(Journal of Philosophi cal Logic)。1983—1989年，第二部逻辑手册《哲学逻辑手册》(四卷)出版，副标题分别为“经典逻辑基础”“经典逻辑的扩充”“经典逻辑的择代”和“语言哲学中的主题”[※注]，体现出哲学逻辑发展到那时为止的理论范围以及与经典逻辑之间的关系，当此之时，也正是逻辑学在计算机科学和人工智能领域获得基础地位的时候[※注]；计算机科学和人工智能以及计算语言学对哲学逻辑的持续需求也直接或间接地推动了这一学科的发展，新的逻辑领域得以建立、旧的领域得到丰富和扩展，第二版《哲学逻辑手册》从2001年开始出版，迄今已经出到第18卷[※注]。2006年，《模态逻辑手册》出版。[※注]这些综述文献的出版从主题上大致厘定了学科范围，既是学科过去发展成就的累积和总结，也为后续进一步研究工作积淀了基础。

数理逻辑和哲学逻辑在哲学、数学、计算机科学以及理论语言学等诸多学科中得到研究；1949年以来，中国逻辑学家们在这些领域中都作出过许多贡献。根据前述文献以及本书的主题和范围，按照年代方式，我们将主要概述国内哲学界在哲学逻辑领域所取得的成果，并力图把它们置于国际逻辑发展的背景之中，尽可能发掘其中的思想源流及其理论意义。为了叙述便利，我们以1978年为界分基础时期(1949—1978年)和发展时期(1978年至今)两个时期，前者侧重概述前17年的成果，后者又分为2000年前后两个阶段，但分三小节叙述——现代逻辑教材建设、重回国际学术舞台(1978—1999年)和融入国际前沿研究(2000年至今)。囿于时间、篇幅和笔者能力，材料搜集可能存在疏漏，概述也可能存在疏漏，敬请读者批评指正！

第二节 基础时期（1949—1978年）

金岳霖(1895—1984年)是第一个在中国系统地传授数理逻辑的人，并且产生了深刻的影响，他要求数理逻辑成为一门独立的科学这一思想倾向，对于数理逻辑在我国的独立发展起了积极的作用[※注]。从1949年开始的17年中，从事现代逻辑研究的工作者很少，其中的哲学工作者更少，“数理逻辑工作的力量极其薄弱，所以具体的研究成果不可能很多。然而理论联系实际的、有生命力的工作已经开始着手了”[※注]。在这一时期，金岳霖的逻辑研究主要反映在他发表的一系列逻辑论文之中[※注]，其中的“客观事物的确实性和形式逻辑的头三条基本思维规律”被他认为是自己“比较得意的”[※注]三篇论文之一。这些工作在当时不仅“以哲学作为一项思想上的武器，为当前国家的需要直接服务”[※注]，而且深入研究了诸如蕴涵、推论、证明[※注]、逻辑的客观基础以及逻辑中心困境[※注]等基本问题。

这一时期，现代逻辑作为我国哲学工作者的一个研究领域，所取得的成就主要在于集合论、逻辑演算、模态逻辑、直觉主义逻辑等方面所建立的演算系统，代表人物为沈有鼎(1908—1989年)；作为我国数学工作者的一个研究领域，主要成就则在于递归论、逻辑演算、模态逻辑、直觉主义逻辑、多值逻辑等方面，代表人物是胡世华(1912—1998年)、莫绍揆(1917—2011年)和王湘浩(1915—1993年)以及他们的学术研究团队[※注]；而对于数理逻辑在新技术中的应用，主要成就在于自动机理论研究和程序自动化研究等方面。当然，这只是一个大致的分类，实际上，各个学科的从业者所取得的成就在上述方向中存在着一些重叠。长期以来，逻辑研究有效推理形式，并最终形成了逻辑演算的概念。国内逻辑演算领域的成果在这一时期涉及经典命题演算、经典谓词演算、模态逻辑和直觉主义逻辑等方面；接下来，我们大致按照时间顺序梳理这一时期的重要成就，然后在本节后面集中梳理多值逻辑领域中的成就。

1950年，莫绍揆发表“演绎定理和两个新的逻辑系统”[※注]，从演绎定理角度建立起避免蕴涵怪论的新逻辑系统。这是莫绍揆的第一篇论文，讨论了逻辑系统中的“蕴涵”与日常生活中的“推理”是否相符的问题，提出可以用一系统中有无“演绎定理”作为相符与否的标准，讨论了三种形式的演绎定理，即如果由假定公式s₁,s₂,…,s_n可在系统S中推出公式p，那么在S内可以推出：(1)s₁→(s₂→…(s_n→p)…)，第一型演绎定理；(2)s₁∧…∧s_n→p，第二型演绎定理；(3)s∧t→p，第三型演绎定理(这里的s为s₁∧…∧s_n,t为证明中使用到的系统S内的公理的合取)。依据这些演绎定理，莫绍揆讨论了几个蕴涵系统，其中一个系统等价于相干逻辑中后来建立的R_→演算[※注]。

经典命题演算和谓词演算方面的主要代表是王世强(1927—2018年)和莫绍揆。在《命题演算的一系公理》[※注]中，王世强指出格托林特(E.Götlind)在1950年提出的命题演算的一组公理不是独立的，该系统包括(1)p ∨p →p;(2)p →p ∨q;(3)p →p;(4)(p →r)→(q ∨p →r ∨q)四条够用的公理，但(1)、(2)和(4)可推出(3)，因此(3)可以省去，其他3条公理是互相独立的，构成一个完全的公理系统。波兰著名逻辑学家拉雪奥娃(H.Rasiowa,1917—1994年)也得到了同样的结果。莫绍揆发表在《符号逻辑杂志》的短文《量化理论笔记》[※注]改进了奎因(W.V.O.Quine,1908—2000年)关于谓词演算的一个论断。奎因曾经指出，如果我们从命题演算及一元谓词演算的形式定理出发，应用广义的蕴涵规则，即由(x₁)…(x_n)A →B和A推出B，可以推出全部谓词演算。莫绍揆指出，只使用通常的蕴涵规则甚至弱化的蕴涵规则，即A →B和A推出B，也可以得出同样的结果。

1953年6月和1955年6月，沈有鼎在《符号逻辑杂志》发表《所有有根类的类的悖论》和《两个语义悖论》。[※注]前者是说，对于类A而言，有一个由类组成的无穷序列A₁,A₂,…(不一定都不相同)使得…∈A₂∈A₁∈A，则称A为无根的。并非无根的类，被称为有根的。令K是由所有有根类组成的类。假定K是无根的，那么有一个由类组成的无穷序列A₁,A₂,…使得…∈A₂∈A₁∈K。由于A₁∈K,A₁就是一个有根类；由于…∈A₃∈A₂∈A₁，因而A₁又是一个无根类，但这是不可能的。所以，K是有根类。因而K ∈K，并且我们有…∈K∈K∈K。因此，K又是无根类。此外，一个类A₁是循环的，仅当存在某个正整数n和类A₂,A₃,…,A_n，使得A₁∈A_n∈A_n-1∈…∈A₁。对于任一个给定的正整数n而言，一个类A₁是n循环的，仅当有类A₂,A₃,…,A_n使得A₁∈A_n∈…∈A₂∈A₁。通过类似的论证可以得到“所有非循环类的类的悖论”和“所有非n循环类的类的悖论”(n是一个给定的正整数)。沈有鼎称这三个悖论是一个“三体联合”，而罗素悖论(所有不是自身分子的类的类的悖论)就是第三个悖论在n=1时的特例。由此可见，非循环类和非n循环类本质上就是有根类，而循环类和n 循环类则是无根类。蒙塔古(R.Montague,1930—1968年)、张清宇(1944—2011年)等人沿着这一方向作了进一步研究。[※注]

两个语义悖论分别简介如下：(1)我正在讲的不可证明。假定这个命题可以证明，那么它一定是真的，用它自己的话说，也就是它不可证明，与假定矛盾。假定它可以证明将引出矛盾，因此这个命题不可证明。换句话说，这个命题是真的。这样，我们也就证明了这个命题。所以，这个命题既可证明又不可证明。(1)的对偶命题是(2)：我正在讲的可以反驳。假定这个命题是真的，或者用它本身的话来讲，它可以反驳。那么它一定是假的，这就跟假定矛盾。假定它可以反驳将引出矛盾，因此这个命题是假的。这样，我们也就反驳了这个命题。弄清这个命题可以反驳，也就是说它是真的。所以，这个命题既真又假。[※注]

沈有鼎提出的这些悖论深刻揭示了直观集合论的缺陷，有助于深化对公理集合论特别是正则公理和分离公理的认识、加强对哥德尔(K.Gödel,1906—1978年)不完全性定理特别是对不可判定命题的理解。[※注]

1955年，莫绍揆改进了[※注]希尔伯特(D.Hilbert,1862—1943年)和贝尔奈斯(P.Bernays,1888—1977年)的命题演算系统M,M包括五组共十五条公理，对各个逻辑联结词的特性表现得很明显，使得推演比较直接，而且可以简明地表现M系统与海廷(A.Heyting,1898—1980年)的直觉主义系统H、约翰逊(I.Johansson,1904—1987年)的极小演算J之间的关系。但是，M系统的五组公理中除否定公理外其余各组公理都不是足够的；一组公理对一个系统而言是“足够的”，是说如果只包含某些联结词的命题是该系统的定理，那么在推演时，除了蕴涵公理外，可限于只用相应于这些联结词的各组公理。瓦伊斯伯格(M.Wajsberg,1902—1942年)证明过H和J的各组公理都是足够的。亨金(L.Henkin,1915—2003年)在1949年对M系统有过改进，但满足公理足够这个要求的代价却是丢失M系统原有的优点。莫绍揆的改进则既使各组公理都是足够的，又保存了原先的优点，所提出的五个改进系统都具备上述三个优点。

沈有鼎是从事数理逻辑工作的哲学工作者。1957年，他在《初基演算》[※注]的论文中认为，命题演算的构成，通常有三步骤的说法，即从约翰逊发表于1936年的《极小演算》到海廷发表于1930年的构造论命题演算再到二值演算。此外，刘易斯(C.I.Lewis,1883—1964年)在1932年的工作中从模态或严格蕴涵出发，也分为了许多步骤，以达到二值演算为终极。特别值得注意的是最后三个步骤，即从S4到S5到二值演算。这两个三步骤就某种意义说乃是通常命题演算的构成中最本质的步骤。综合这两个三步骤，会带来许多便利，而沈有鼎所提出的也就是作为二者共同基础的初基演算。这个“初基演算”是比约翰逊的极小演算还小的演算。初基演算可以看作是极小演算和刘易斯的S1的“交”的一部分，它有两个基本推理模式：(Ⅰ)从A和A →B推出B;(Ⅱ)从A和B推出A ∧B。其公理模式有14条：

(1)A→A；

(2)(B→C)→(A→(B→C))；

(3)A∧(A→B)→B；

(4)(A→B)∧(B→C)→(A→C)；

(5)A∧B→A；

(6)A∧B→B；

(7)(A→B)∧(A→C)→(A→B∧C)；

(8)A→A∨B；

(9)B→A∨B；

(10)(A→C)∧(B→C)→(A∨B→C)；

(11)A∧(B∨C)→(A∧B)∨(A∧C)；

(12)(A→B)∧¬B→¬A；

(13)A→¬(B∧¬B)；

(14)A∧¬(A∧B)→¬B。

在初基演算中把公理(2)加强为：

(2′)B→(A→B)

所得到的系统就是“极小演算”。在初基演算上增加公理“(A∨B)∧¬A→B”所得到的系统是S4与海廷直觉主义命题演算相交叉的一部分，沈有鼎称为“次基演算”。在次基演算中把公理(2)加强为(2′)，所得到的系统就是直觉主义命题演算。在次基演算上增加公理“A→B∨¬B”，所得到的系统就是刘易斯的S4。在S4上增加公理：

(*)¬(B→C)→(A→¬(B→C))

所得到的系统就是刘易斯的模态系统S5。在S5中把公理(2)和(*)加强为(2′)，所得到的系统就是通常的二值命题演算。

初基演算反映了三个系统的关系，其中的两个就是带模态词的命题逻辑系统S4和二值命题演算，两者有同一个来源，只是得到不同的强化或增补才出现了差异，而强化或增补过程中没有一个步骤使得我们怀疑它们的完全性，我们完全有理由把模态逻辑和二值逻辑视为同类。也就是说，沈有鼎的初基演算建立起了标准逻辑的两个标准，即是否起源于初基演算和是否具有完全性，这些工作对当前关于“逻辑性”的哲学研究依然具有重要意义。莫绍揆在两年后认为，沈有鼎的初基演算可以说是用直觉主义眼光来讨论模态系统，也可以说是用模态的观点来推广直觉主义系统，是一个新尝试，是一条很可继续研究的道路，他在公理的选择上对初基演算加以改进，提出了三个改进的初基演算系统[※注]。2000年，刘壮虎建立了初基演算的邻域语义学并证明了对于这一语义的完全性定理。[※注]

1957年，莫绍揆研究了一些具有有穷个模态辞(由命题变元以及否定词、可能模态词、必然模态词三种运算所组成的命题)的模态系统[※注]，从一个基本模态系统B出发，研究具有有穷个模态辞的模态系统，使每一模态辞¬□supa1¬□supa2¬…¬□supan都对应于数列a₁,…,a_n，并根据模态辞之间的蕴涵、等价规定数列间的顺序、相等，这样就可以把模态辞个数的研究代数化，使讨论更便利和有系统地进行。此后，他继续这一方向的工作[※注]，研究了一般构造有穷模态系统的问题，得到了部分结果。

1959年，模态逻辑和直觉主义逻辑领域还有两个重要工作。第一，模态逻辑方面。莫绍揆讨论了模态系统之间的关系[※注]，得到以下结果：(1)把当时已有的模态系统(卢卡西维茨的系统除外)的共通部分称为基本系统，这是最弱的系统，按照各种方式加强得出各种加强系统，共有60余种，而通常的模态系统都包含在内；(2)比较了刘易斯的S1—S5，其中S2、S3和S4都属于上述加强的系统，S5不在范围之内乃是因为它有叠置模态词，S1不在其中则表明S1有缺陷；(3)古典二值逻辑使用了实质蕴涵而产生蕴涵悖论，导致刘易斯使用严格蕴涵从而产生出现代模态逻辑。莫绍揆在前面讨论的模态系统都还存在着蕴涵悖论，因此，他提出一个蕴涵系统，在这个系统中，蕴涵词和模态词的性质都和直觉相符但蕴涵悖论消失了。第二，直觉主义逻辑方面。海廷的直觉主义系统H容许“从矛盾可推出任何命题”，招致约翰逊的批评，约翰逊发展了极小演算J，但是J中却没有以下关系(甲关系)：在古典系统内能够推出命题p时，在该系统内恒能推出¬¬p；逆亦真。莫绍揆把直觉主义系统定义为与古典系统之间成立甲关系的系统[※注]。据此，极小演算不是直觉主义系统。但是极小演算具有以下性质：对于任何形式定理，如果将其中每一形如¬p的部分命题替换为p →q，那么所得的命题也是该系统内的形式定理。他把具有这种性质的系统称为普否系统，在论文中发展了很多种具有不同特点的普否系统，其中既包含极小演算又具有普否性质的系统是最为合适的一种直觉主义系统。然后，普否系统被推广为共否系统。共否系统即其中一个系统具有带否定符号的定理时，另外一个系统必定也带有相同奇偶数的否定符号的定理。在极广泛的假设之下，互为共否的系统必定共同否定同样的命题。莫绍揆证明，归约的或开展的互为共否的系统中，如果有普否系统存在，那就一定是唯一的。归约系统是指具有以下性质的系统：如果¬¬¬p是定理，那么¬p也是定理(弱归约)；如果¬¬p是定理，那么p也是定理(强归约)。开展系统是指具有以下性质的系统：如果p是定理，那么¬¬¬¬p也是定理(弱开展)；如果p是定理，那么¬¬p也是定理(强开展)。

逻辑中有一个确定含有数的量词的普遍规律的部分，称为“假变项理论”或“函项演算理论”，其实就是量词演算。1964年，莫绍揆讨论了谓词演算中的枚举量词[※注]。枚举量词是以下这样的量词：

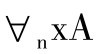
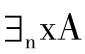
n级恰有量词Λ_nxA(x)：恰巧有n-1个x使A(x)成立。

莫绍揆认为，直到那时为止，数理逻辑学家通常都是把关于枚举量词(及摹状词)的讨论建基于同异性演算之上的，有关枚举量词(以及摹状词)的定义及其公理，都是借助于同异性“=”来表达的。因此照通常的做法，一级谓词演算被分成三个部分：1.(通常的)全称、存在量词论；2.同异性演算；3.枚举量词及摹状词论。这样的处理方法有些缺点，他建议把以往的讨论方式加以更改：先发展枚举量词及摹状词论(它们恰好合成完整的纯狭义谓词演算)，然后再在枚举量词论之上而发展(第一型的)同异性演算，将是较合理想的做法：如果想和现在的处理方式相距不致太远，可先发展一级全称存在量词论再发展唯一性量词论，在唯一性量词论上发展第一型的同异性演算，以后再发展枚举量词及摹状词论。虽对同异性演算作了改进，但狭义谓词演算仍被分成两段。

1959年，金岳霖、胡世华、王宪钧(1910—1993年)参加《十年来的中国科学·数学》的编写工作，执笔撰写的“数理逻辑”列于华罗庚(1910—1985年)等撰写的“总论”之后第一章，包括“引言”“十年来的历史发展”“研究成果的综述”(分为演绎逻辑系统、多值逻辑、能行性问题和数理逻辑在新技术中的应用)和“文献”四个部分，指出“数理逻辑在我国的这十年是讨论、争辩并经过实践不断明确自己任务和工作方向的十年”[※注]。从1949年开始的17年，这段时期是我国数理逻辑(包括哲学逻辑)研究的基础时期，这种“基础性”主要体现在以下几个方面：第一，我国数理逻辑学者如沈有鼎、胡世华、莫绍揆和王湘浩等人发表了具有国际水准的学术成果，这些成果主要体现在哲学逻辑演算系统的建立、数理逻辑(递归论)中的能行性问题研究以及逻辑哲学等方面，其中大部分工作将为国内学界后来的研究奠定良好的基础；第二，这个时期培养了一些具有良好基础的数理逻辑工作者，为我国数理逻辑在将来的发展奠定了良好的基础；第三，我国数理逻辑工作者形成了若干个科研群体，这些群体的研究方向比较明确，在各自领域内既有学术带头人，也有核心研究人员。[※注]

第三节 发展时期（1978年至今）

1978年5月15—21日，中国社会科学院哲学研究所和《哲学研究》编辑部在北京组织召开了第一次全国逻辑研讨会，国内100多位逻辑学工作者参加了会议，金岳霖出席了开幕式并作了书面发言，认为“这是值得我们庆祝的大事……这个会是逻辑工作者的学术讨论会”[※注]。一些数理逻辑学家在会上以学术报告形式对数理逻辑作了比较全面的宣传：《作为现代逻辑学的数理逻辑》(胡世华)、《数理逻辑和形式逻辑》(王宪钧)、《传统逻辑与数理逻辑》(莫绍揆)、《可计算性理论的发展及其应用》(吴允曾)、《推理与计算》(张锦文，1930—1993年)和《二十世纪逻辑学的发展》(张尚水)；后者随即发表在8月的《哲学研究》，为数理逻辑、哲学逻辑以及数理逻辑与哲学之间的关系提出了一个精致的简史[※注]。

在此前后，世界著名逻辑学家、哲学家王浩(1921—1995年)多次访华，在北京、上海和南京等地作了大量数理逻辑前沿讲座，《哲学研究》《北京大学学报》和《国内哲学动态》等刊物对这些讲座作了大量报道[※注]。1977年10月，他在中国科学院计算技术研究所作了六次大型讲座，讲稿《数理逻辑通俗讲话》则由14位数理逻辑学家翻译校对、由科学出版社在1981年出版并于1983年重印，包括八章正文“数理逻辑一百年”“形式化和公理方法”“计算机”“问题与解”“一阶逻辑”“计算——理论的和可实现的”“直线上有多少点？”“统一化与多样化”和三章附录“骨牌游戏与无穷性引理”“算法与机器”和“抽象机”。这部著作对数理逻辑的基本内容作了大体自足的讲述，篇幅不多而内容非常丰富(不少章节包含有王浩自己的工作)，金岳霖题写了书名，莫绍揆、吴允曾等人发表了多篇书介以助于理解[※注]，这些都使得该书在国内学界的影响非常深远。

此见青蓝，薪火相传。凡此种种，为逻辑学工作者接续之前数理逻辑、哲学逻辑在国内的发展起了积极的推动作用，老一辈数理逻辑学家继续之前的研究工作，而且“在1978年后恢复了研究生培养制度，培养出一批学有所成的数理逻辑工作者。我国年青一代的数理逻辑工作者日渐成长，成为我国数理逻辑科研领域的骨干力量”[※注]。

一 现代逻辑教材建设

逻辑研究和逻辑教育相辅相成。“昨天的教育满足不了明天的需要”[※注]，逻辑教育涉及逻辑教材建设，这是一个深及逻辑本质和逻辑观念的工作，因为“除了任何定义中包含的困难外，我们并不确切地知道逻辑是什么，我们不能在任何严格程度上定义它。但是，也许我们大多数人都对逻辑教科书的主要内容留下深刻印象”[※注]。

在第一次全国逻辑研讨会的报告中，王宪钧提出，“国内现在有关数理逻辑的读物太少，我们应该大力组织出版这类读物。最好能够写出几套教材，为数学工作者的，为计算机科学工作者的，也要写一套为逻辑和哲学工作者的”[※注];1982年，他在20世纪60年代完成的讲稿基础上增补出版了广为称引的《数理逻辑引论》，其中第三篇“数理逻辑发展简述”以8万字篇幅论述了数理逻辑从莱布尼茨到哥德尔的三个发展阶段，是我国学者撰写的第一部数理逻辑史专论，影响深远[※注]；随后主编的“现代逻辑丛书”在90年代初陆续出版，目的是提供一批叙述简明易懂和不需要较多数学知识的入门性书籍和教材：《西方形式逻辑史》(宋文坚著)、《逻辑演算》(刘壮虎著)、《一阶逻辑和一阶理论》(叶峰著)、《模态逻辑》(周北海著)、《集合论导引》(晏成书著)和《递归论导引》(郭世铭著，1946—2000年)；原在计划之内但出版时没有列入丛书的有《模型论导引》(沈复兴著)、《素朴集合论》(刘壮虎著)。1986年，周礼全(1921—2008年)出版写成于70年代后半期的《模态逻辑引论》[※注]，最后一章“模态逻辑简史”叙述了模态逻辑从亚里士多德至20世纪60年代的发展史，这是我国学者撰写的第一部模态逻辑史专论。1990年，张尚水出版《数理逻辑导引》;1993年，宋文淦出版《符号逻辑基础》，张家龙出版《数理逻辑发展史——从莱布尼茨到哥德尔》。

1993年，康宏逵(1935—2014年)编译出版了模态逻辑文集《可能世界的逻辑》，指出模态逻辑的复兴是当代逻辑学最重要的新发展，它是哲学逻辑大批分支的凝聚点，长篇代序“模态、自指和哥德尔定理：一个优美的模态分析案例”写成于1990年，全部内容89页约6万字，相当于一部观点鲜明、内容深刻的小型专著，是这一时期国内数理逻辑领域最重要的著作之一。[※注]

在《逻辑学的传入与研究》中，宋文坚写道，“80年代前，我国没出版过一本数理逻辑专著，科研论文也很少。……而这个时期欧美的逻辑界在现代逻辑前沿问题上成绩辉煌”[※注]。改革开放之后，经过几代逻辑学者的共同努力，国内逻辑学界这一境况开始有所好转。

二 重回国际学术舞台（1978—1999年）

从1978年开始，莫绍揆在经典逻辑演算方面继续发表了一系列论文，涉及逻辑函词演算、改进二阶谓词演算以消除悖论、无类型的完备逻辑演算、直觉主义逻辑、极小演算以及元逻辑研究等方面，兼涉数学基础问题。[※注]1981年，沈有鼎发表《“纯逻辑演算”中不依赖量词的部分》[※注]，从带等词的一阶逻辑中分离出一个完全的、可判定的子系统。“纯逻辑演算”专指加入了“同一”概念之后的狭谓词演算，纯逻辑演算中不依赖量词的部分是纯逻辑演算中极其微小的部分。这篇论文采用一种与命题演算中运用真值表判定一公理是否定理的方法相类似的判定方法，把真值表推广为值表，这种方法本身可以理解为一种公理系统；它以条件析取“〔A,B,C〕”为初始概念，括号记法承续丘齐(A.Church,1903—1995年)的工作，此后由张清宇等人在关于经典逻辑和模态逻辑的工作中作了进一步发挥，并为2010年提出的肖菲克尔(M.Schönfinkel，1889—1942年)型算子建立起新的公理系统、建立起与维特根斯坦(L.Wittgenstein,1889—1951年)的N 算子及一些可判定模态逻辑的联系[※注]。

80年代初期的第一版《哲学逻辑手册》对国内哲学领域中的逻辑学工作者所带来的影响应该是巨大的，大部分研究工作都将在这个文献的基础上开展。

1988年，《哲学逻辑杂志》发表了徐明的硕士学位论文《一些U,S时态逻辑》[※注]，是这个时期我国逻辑学工作者重返国际逻辑学术研究舞台的早期工作。时态逻辑始于50年代普莱尔(A.Prior,1914—1969年)的工作，1968年，坎普(J.Kamp)在博士学位论文中添加了两个新的二元联结词S(since，自从)和U(until，直到)，并且证明：关于戴德金完备的严格全序来说，U和S 是表达完备的。自从/直到逻辑的建立是模态逻辑研究中一个重大突破。伯吉斯(J.Burgess)在1982年为线序类和稠密及离散序的类建立起公理系统，完全性证明使用了模态逻辑完全性理论文献中所说的“逐步构造(step-by-step)”[※注]方法，但把某种演绎封闭集巧妙地运用在“逐步构造”的过程当中；徐明把这些方法应用到(可能)非线性时间的一般情形并且提出了一些关于U、S时态语言的表达性结果，在前一个工作中，证明了极小的U、S-时态逻辑 TL_US(f)的存在，也建立了所有传递框架类和所有传递的左连通框架类等的“分叉时间”的逻辑。他们这些关于线序时间类的公理在时态逻辑文献中被称为“伯吉斯—徐公理”[※注]。此后，徐明还在stit逻辑、条件句逻辑、道义逻辑和模态逻辑等领域中做了很多工作。[※注]

20世纪60年代，达·科斯塔(N.da Costa)创立弗协调逻辑。从1991年开始，张清宇发表“一个弱的弗协调条件句逻辑”和“弗协调模态逻辑C_nG′,n ∈ω”，并且与达·科斯塔合作发表“弱的弗协调条件句逻辑C_nW”；第一篇论文将巴坦思(D.Batens)在1980年建立的弗协调逻辑系统PI和弱条件句逻辑系统组合成一个弱的弗协调条件句逻辑PIW；第二篇论文建立的弗协调模态命题逻辑C_nG′是一个正规弗协调模态逻辑，包含达·科斯塔建立的弗协调逻辑系统C_n的全体定理，其完全性证明概括了很大一类正规弗协调模态命题逻辑的完全性；第三篇论文将C_n和弱条件句系统W组合起来得到一个完全的系统C_nW。这些工作把弗协调逻辑引进到国内研究范围并以之与国际学界联系起来[※注]，此后，国内从事弗协调逻辑研究的年青一代逻辑学工作者大都深受这些工作的影响。

在时态逻辑方面，1992年，王学刚为具有通常形式语义的时态算子H、G、H′和G′的任意序的类建立了一个极小的时态逻辑系统L₀′，并用演绎封闭集合极大一致集方法证明了系统的完全性定理。随后，张清宇把这个极小系统和达·科斯塔的系统C_n组合成一个弗协调G′、H′-时态逻辑[※注]。

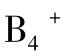
无穷逻辑是经典一阶逻辑在表达力方向上的扩张。李小五在1993年的论文中指出，协调性质这个概念是为解决经典一阶逻辑的问题而在1963年由斯穆里安(R.Smullyan,1919—2017年)提出，在70年代初，基斯勒(J.Keisler)讨论了协调性质与无穷逻辑语言L_ω1,ω的关系，并证明了用 L_ω1,ω表述的无穷逻辑关系 B_ω1,ω的完全性，巴维斯(J.Barwise,1942—2000年)把协调性质概括到L_∞,ω情形，得到了L_∞,ω的片段的完全性定理和其他结果。李小五把协调性质概括到L_κλρπ(基数κ、λ、ρ、π使κ是无穷正则基数或是共尾度为ω的奇异基数且ω≤λ≤κ。如果λ是奇异基数，那么ρ是＜λ的正则基数，如果λ是正则基数，那么ρ≤κ,π≤κ)的情况，并且用语言L_κλρπ表述他建立的几个以B为基础的无穷公理系统，证明了这些系统的完全性定理。随后，他出版了两卷《无穷逻辑》，并转入条件句逻辑的研究。[※注]

邻域语义学是70年代初由蒙塔古和斯科特(D.Scott)提出来的。这种语义学的主要特点就是把命题之间的联结词都看作以命题为变元的函数，由该联结词联结的复合命题在某个可能世界上的真假情况由支命题的真假情况决定。如果复合命题在某个可能世界中的真假情况仅仅由支命题在这个可能世界中的真假情况能够确定，那么这个复合命题中的联结词就是外延的；一般情况是，为了确定一个复合命题在一个可能世界中的真假，不仅要考虑支命题在这个可能世界中的真假情况，还要考虑支命题在其他可能世界中的真假情况，这样的联结词具有内涵性质。邻域语义学把所有的命题联结词统一当作命题算子(用函数加以刻画)来处理。从1995年起，刘壮虎发表了一系列论文研究邻域语义学。在《邻域语义学和模型完全性》中，他提出了一般的命题形式语言和命题推演系统，建立起命题推演系统的邻域语义学，提出命题推演系统在邻域语义学中的几种不同的完全性，即模型完全性、弱模型完全性和框架完全性，运用典范模型方法给出了一个命题推演系统有模型完全性的充分必要条件，并且证明了任何命题推演系统都具有弱模型完全性。随后，他将邻域语义学推广到模态谓词逻辑，讨论了模态谓词逻辑的框架完全性，给出了模态谓词逻辑中巴肯公式在邻域语义学中的一个形式特征。这些工具和技术被毛翊具体应用到条件句逻辑完全性定理的证明。2008年，在和李小五合作的论文中，他们建立了主次条件句的极小系统 C2 L_m，根据邻域语义学引进了一般的典范模型概念，然后应用典范模型证明了系统的完全性。此外，在2008年发表的论文“有限全序语义和广义皮尔士律”中，他将二值逻辑中刻画实质蕴涵的保真性推广至有限全序中，用这推广的“保真性”给出蕴涵在有限全序中的语义条件，从而给出了完整的有限全序语义，在建立刻画有限全序的逻辑系统 FO之后，证明了FO的完全性和可判定性；此外，论文提出广义的皮尔士律，证明其能区分不同基数的有限全序，然后给出了 FO 的扩充系统FO_n并证明了FO_n刻画了n个元素的全序。[※注]

我国是逻辑学发展最早的国家之一(《墨子》一书中的“小取”篇是一篇内容丰富的逻辑著作)，在吸收外来文化上也有优良传统(唐代玄奘介绍印度的逻辑学，即“因明”)。1980年，沈有鼎结集出版了《墨经的逻辑学》；从1994年开始，张清宇在此基础上创制出一系列组合了词项逻辑和命题逻辑的名辞逻辑系统MZ、MC和MD,《墨经》的逻辑学说在这些工作中起了重要作用。1998年，张家龙运用经典一阶逻辑刻画了《墨经》中“侔”式推理的有效式。[※注]这些工作和其他人的工作一起揭示了中国古代逻辑，尤其是《墨经》逻辑可以达到的形式化高度及其有所欠缺之处，目前开始被介绍给国际逻辑学界。[※注]

1995年，“第十届国际逻辑、方法论和科学哲学大会”在意大利的佛罗伦萨举行，王路在会议报告中介绍了徐明、王学刚和张清宇3个人关于时态逻辑和弗协调逻辑的6篇英文论文，并且说：“在中国，我们在研究中有一个很大的缺陷，那就是我们缺乏与国外进行学术交流。”[※注]这一“缺陷”将在21世纪得到很大改观。1999年，周北海在《符号逻辑杂志》发表《嫁接框架和S1的完全性》。[※注]

三 融入国际前沿研究（2000年至今）

2000年，王路出版《逻辑的观念》[※注]，从“逻辑”这个名称的不同含义、不同逻辑教材的不同内容和不同逻辑史著作的不同内容出发，寻找其中共同的东西，探讨其内在机制。王路指出，逻辑的内在机制是指决定逻辑这门学科得以产生和发展的东西，在逻辑的发展中贯彻始终。围绕着逻辑的内在机制是“必然地得出”这一基本思想，他论述了逻辑这门科学的性质、范围以及逻辑和哲学的关系等一系列问题，指出逻辑在20世纪分析哲学和语言哲学中的重要作用以及逻辑对于理解西方哲学的必要性，等等。这些思想从观念上对国内逻辑学家造成了很大影响，从而推进了1978年以来国内逻辑教学和研究现代化的进程。2016年，他自己在研究亚里士多德逻辑、弗雷格逻辑和模态逻辑的基础上出版《语言与世界》[※注]，构建了一种新的解释模式“句子图式”，用以对弗雷格的含义和意谓理论、罗素的摹状词理论、克里普克(S.Kripke)的因果命名理论、奎因对分析与综合判断区别的质疑、盖提尔(E.Gettier)论题、维特根斯坦的事实构成世界论等作出了系统的新解释。

进入21世纪以后，哲学院系中年青一代逻辑学工作者在老一辈逻辑学工作者的指导下也开始成长起来。几代学人在哲学逻辑很多分支的前沿问题上都有所研究和贡献，国际交流与合作也日趋普遍。

从2003年开始，周北海、毛翊和张立英等发表出版了一系列关于概称句语义解释和推理的论著。区别于经典逻辑研究的完美形式的数学推理，日常生活中常用的常识推理是非单调的，即前提增加时其结论可能会被收回。日常生活中大量使用的既表达普适性规律又容忍例外的概称句推理是一种非单调推理，就这种非单调推理来说，概称句是导致非单调性的本质原因。2004年，周北海提出概称句是表达概念内涵的句子，形成概称句的概念式理解，在此基础上，于2008年建立了概称句的含义语义，得到概称句的词项逻辑GAG与Gaa，这两个逻辑分别是关于从概念到概念推理的逻辑和从概念到个例推理的逻辑，对这两类概称句推理及逻辑给出了合理的解释和刻画，判定算法和完全性定理证明在随后的工作中完成。对应用模态逻辑和条件句逻辑的技术和方法，周北海和张立英对概称句的语义解释和概称句推理进行了系统研究，基于概称句的语义解释(双正常语义)给出了一批原创性的结果，包括结论是概称句的推理(演绎部分和归纳部分)以及概称句推理与归纳关系的讨论、概称句视角下的休谟问题等。在概称句推理部分，张立英给出了5个有不同直观的概称句推理逻辑系统G0-G4并证明了系统的完全性。[※注]此外，在相干逻辑方面，周北海和贾青合作发表了一批研究成果。[※注]

2003年，余俊伟在张清宇关于弗协调模态逻辑工作的基础上提出“一个弗协调真值道义逻辑系统”并发表在《哲学研究》，按照通常的做法添加常项和公理，而将道义逻辑归约为弗协调真值模态逻辑，建立了一个可靠和完全的C_nMG′，以之解决善良的撒玛利顿人悖论。2004年，他建立了一个极小的弗协调逻辑系统，是从C_ω′中去掉双重否定律后所得到的、比达·科斯塔弗协调逻辑系统C_ω′更小的系统，证明了该系统相对于克里普克语义解释的可靠性和完全性定理。[※注]

计算机科学的发展在21世纪进入了知识处理和智能模拟阶段，构造逻辑系统描述认知过程，进而实现知识表达和处理，已经成为逻辑学的主要研究任务之一。由于时空条件的限制，认知主体始终处于知识不完备状态。因此，克服逻辑全知者假定，恰当地刻画认知主体的信念推理结构，这是国际逻辑学界和人工智能学界所共同关心的问题。在这一方向上，费京(R.Fagin)等人的广义觉知逻辑被公认为最重要的解决方案，并由此创建哲学逻辑的一个新分支——觉知逻辑。但是，由于该方案没有考虑到觉知概念本身的复杂性，忽略了觉知状态与信念推理间复杂的相互关系。2004年，鞠实儿和刘虎在《哲学逻辑杂志》发表的“二维觉知逻辑”提出了研究觉知逻辑的新方法，并据此建立了新觉知逻辑系统。这篇论文独创性地使用二维逻辑方法研究觉知逻辑，构造不同的逻辑系统，多层面地刻画觉知概念，从而扩充了觉知逻辑的表达能力。论文首次将二维逻辑与模态逻辑相结合，给出了二维模态逻辑的形式系统，并发展出证明二维模态逻辑完全性的方法。具体地说，该论文将语言学中对预设问题的研究结果引入信念逻辑的研究中，表达预设的二维逻辑被用于建立各种觉知—信念模型。2013年，刘虎和文学锋发表合作论文《恒常联系理论基础上因果的形式化》，给出了基于经验学习的因果逻辑，并探讨这种逻辑的哲学意义和应用价值。20世纪以来，逻辑学家为诸多哲学概念建立了形式化逻辑系统，形成了哲学逻辑这一分支繁多的研究领域。但是，对于因果关系这个核心的哲学概念，仍然没有一种统一的因果逻辑可被逻辑学界广泛接受。他们这篇论文致力于改变这种现状，确立因果逻辑作为哲学逻辑分支的地位。论文给出的因果逻辑以肇始于休谟的因果关系的恒常联系理论为基础。恒常联系理论曾经统治因果关系的哲学理论200多年，但在近代逐渐式微，让位于反事实条件句理论。近年来，国际哲学界兴起一股回到恒常联系理论的思潮，该论文为重新确立恒常联系理论提供强大的理论支持。在因果逻辑中，形式化的分析方法使我们能够明晰恒常联系理论的理论预设、概念结构和推理性质，从而使我们能够更清楚地看到它优于反事实条件句理论之处。后者已有较为完整的形式化理论。现有的基于反事实条件句理论的逻辑有着内在的系统缺陷，如承认因果关系在演绎后承下封闭等。因此，它们不能被学界广泛接受为因果逻辑。该论文的研究表明，因果关系不是一个独立的概念，它依赖于时间概念和事件的影响范围概念。因果关系陈述的真假，依赖于我们对过去经验的审视。以此出发建立的逻辑系统，能够克服原有逻辑的缺点，从而使一种真正的因果逻辑成为可能。[※注]

2008年，熊明在《哲学逻辑杂志》发表《经典逻辑的直觉主义刻画》，通过引入内涵映射及其性质而为刻画中间逻辑建立了一个新的语义方法。在此前后，他在真理论和悖论等方向做了很多工作。2017年，他发表《布尔悖论和修正周期》一文，基于古普塔(A.Gupta)、贝尔纳普(N.D.Belnap,Jr.)和赫兹伯格(H.Herzberger)等人的真之修正理论，利用其中的修正周期作为刻画悖论的主要参量，并在作者提出的相对化T模式下，对一类称为布尔悖论的真理论悖论进行分析和刻画。分析表明，布尔悖论具有良好的对角线结构，在形式算术理论中具有一致的形式表达，其基本的语义特征——修正周期——与其矛盾性和矛盾程度的高低(悖论度)有密切的关系。由此建立了一系列的有关布尔悖论的形式构造和形式刻画方面的结果，揭示出这一类悖论在悖论度上具有的层次性和复杂性，使我们对悖论的认识有新的推进。具体成果概述如下：(1)在形式算术中完成布尔悖论及其相关系统的一个完全的形式构建，把哥德尔创立的对角线方法与修正理论中的修正序列及其周期特性进行结合，给出了一种从修正周期构建悖论的一般方法，扩大了悖论的研究范围。(2)基于塔斯基T模式在可能世界上的一个模态版本，利用布尔悖论的修正周期特征对它们的矛盾性给出了完全的刻画，建立了这些悖论之间关于悖论度的一般性的比较性结果。(3)在以上两个成果基础之上，最终证明了布尔悖论在悖论度的结构上是一个无界的稠密格，这一方面反映出布尔悖论作为一种逻辑对象具有良好的代数结构，另一方面也反映出布尔悖论本身的丰富性和复杂性，也间接反映了真作为一个循环性概念的难解性，这对于真的哲学分析提供了一个新的逻辑理论框架。[※注]

20世纪60年代初，由麦金森(I.Makinson)与克雷斯韦尔(M.Cresswell)首先引入模态逻辑的典范性概念被莱蒙(E.Lemmon,1930—1966年)与斯科特(D.Scott)大规模用于证明完全性定理，直到今天它还是常规的方法；范启德(Kit Fine)发表于1973年的工作以及对与之相关问题的探讨，开启了模态逻辑典范性问题研究这一方向。从2009年开始，裘江杰在这一方向上发表了一些研究成果：在典范框架方面，证明了极小正规逻辑K的典范框架中存在着连续统多个在有穷步通达到死点的元素，对于典范框架的全景视图增加了新的细节；对典范框架上的拓扑结构作了相应的讨论；得到了典范框架中有界宽的生成子框架是相应逻辑的框架等结果；在典范公式和典范公理化方面，证明了由萨奎斯特(H.Sahlqvist)公式公理化的逻辑组成的类是一个其中有无穷长的链与反链的格。[※注]

在模态逻辑的格论研究中，从2011年开始，康宏逵和杜珊珊陆续发表了一批成果。在《模态镜子里的反欧性》[※注]中，他们用戈德布拉特—托马森定理证明了反欧性一般来说是模态不可反映的，由此找到了最小的反欧传递逻辑，并且证明了所有的反欧传递逻辑不仅具备有穷框架性，也都是可有穷公理化的，继而也都是可判定的；论文最后研究了反欧传递逻辑格里的濒表格逻辑，给出了几个具有“临界性”濒表格扩充的逻辑的实例。2014年，他们发表了两篇论文研究关于NExtK4的濒表格逻辑[※注]，证明了传递逻辑格中的濒表格逻辑的判据及其应用结果：第一篇论文提出“点式归约”以及“在点式归约下的不变性”这两个重要的新概念证明了传递逻辑格中有穷深度濒表格逻辑的判据，还给任意传递框架到它自身中的归约作了穷尽的分类(传递框架间的真点式归约有并且只有5种)；第二篇论文证明了传递逻辑格中无穷深度濒表格逻辑的判据，同时结合第一篇文章所得判据，将濒表格逻辑的判据研究结果应用到NExtQ4这个传递逻辑格的子格上，得到了关于该格的濒表格逻辑的基本结果，即NExtQ4与传递逻辑格相仿，它同样有连续统多个无穷深度的濒表格逻辑。“点式归约”以及“在点式归约下的不变性”这两个概念再次起到了重要作用。从问题的来源来看，这两篇论文的工作实际上延续了80年代以来布洛克(W.Blok,1947—2003年)在传递逻辑格(由K4所有正规扩充构成的逻辑格)上关于顶部逻辑——濒表格逻辑(其正规的真扩充都是表格逻辑的逻辑)的相关判据的研究结果，给出了一个关键的统一而非分散的判据，这是传递逻辑格研究方面的理论意义。

冯棉在2011年和2012年发表了结构推理的一些成果，此后又研究了相干与衍推谓词逻辑。命题逻辑的一般弱框架择类语义是相干邻域语义的变形，特点是采用择类运算来刻画逻辑常项、语义运算与逻辑联结词之间清晰的对应关系。在论文《一类命题逻辑的一般弱框架择类语义》中，冯棉将这种语义用于一类B、C、K、W命题逻辑，包括相干逻辑R及其线性片段、直觉主义逻辑及其BCK片段等，并借助典范框架和典范赋值，证明了这些逻辑系统的可靠性和完全性。另外，从结构推理的观点来看，结合演算是一种很弱的逻辑，因为它仅容纳一种结构规则，即“结合规则”，正结合演算作为一种“正命题逻辑”，是结合演算的基础。在“正结合演算”中，他构建了正结合演算结构推理系统BL和对应的公理系统B，阐述了结合演算拒斥“交换规则”“收缩规则”和“弱化规则”的理论意义和应用价值，证明了系统 BL和系统B的等价性。[※注]

数学基础问题是数理逻辑诞生的主要动机之一，也是数理逻辑研究的一个主要领域。叶峰指出，迄今为止的科学所认识的世界是有限的，从微观的普朗克尺度到有限的宇宙尺度，经典数学在科学中的应用都是用无穷模型来近似地模拟有限事物。关于数学的可应用性方面存在一系列逻辑问题，如无穷对于描述有限世界是否是逻辑上绝对不可或缺的，应用无穷模型进行模拟时在逻辑上如何保持对有限世界的真理性，数学在科学中的应用是否可能表达为从关于有限物理对象的真前提到关于有限物理对象的真结论的、纯逻辑有效的推导。在2011年前后的一系列工作中，他提出了一个严格有穷主义的逻辑系统SF[※注]，证明了一部分经典应用数学(包括经典量子力学和广义相对论的数学基础)可以在这个系统中发展起来，由此说明经典数学在科学中的应用，原则上可以转换为从关于有限物理对象的真前提，到关于有限物理对象的真结论的逻辑有效的推导，从而从逻辑上解释了为什么用表面上谈论无穷数学对象的经典数学可以帮助推导关于有限物理世界的真理。SF是无量词的初等递归算术，它有自由变元但不用量词，所接受的自然数函数都是初等递归函数，可以完成哥德尔编码，用类型化的兰姆达演算记号但不真正假设存在函数、函数的函数等高阶实体，兰姆达演算的项被解释为计算程序而且都是初等递归的程序。哲学工作者中从事数学基础问题研究的还有邢滔滔、郝兆宽、许涤非、杨睿之等。

2011年，刘奋荣出版《偏好动态学的推理》[※注]，其中一部分内容同年发表在《哲学逻辑杂志》，为“偏好”概念提出了两个新的逻辑模型。第一，模态的模型。这个模型采用动态认知逻辑的方法，先给出了静态的模态偏好逻辑，其中的偏好是可能世界上的一个偏序关系，在形式语言中由模态词表示，然后在这个系统中添加偏好变化的动态算子，例如“公开建议”，从而得到动态偏好逻辑。动态偏好逻辑给出了主体接收新信息前后偏好变化的规律，这体现在动态的归约公理中。由于归约公理都是等价的公式，动态偏好逻辑系统的完全性通过归约公理可以由静态偏好系统获得。此外，她在这个模型中探讨了如何将动态的偏好变化抽象理解成一种关系的变化，利用命题动态语言来描述可能的、更为复杂的偏好变化。这样，归约公理可以自动推导出来。第二，一阶的模型。这一方向中先前的著作大多将偏好作为初始概念，很少考虑偏好是如何产生的问题。刘奋荣认为，谈论偏好不仅与我们关于讨论对象的性质的认识有关，还与这些性质对我们而言的重要性排序有关，这就是所谓的优先序。就形式而言，她利用一阶语言的片段定义了偏好关系。在这个模型中，优先序上的动态变化直接导致偏好的变化。刘奋荣重点研究了几种情况：增加新性质、性质的重要性发生改变、剔除最不重要的性质。这三种情况分别对应逻辑语言中的三个动态算子，书中给出了这些算子对应的归约公理。在基于优先序的偏好模型中，该书证明了一系列“表征定理”，它们表明，任何偏好的性质和变化都能在优先序中找到表征。这两个模型基于不同的直观、分别使用模态语言和一阶语言，但对偏好的原因和动态变化给出了形式的建模。在比较、进一步抽象这两个模型的基础上，她提出了偏好的双层理论，即在同一个模型中同时包含两个构件，一个是偏好的层面，另一个是偏好的原因层面，就语义而言，前者对应的是可能世界上的偏好关系，后者对应的是可能世界集合上的关系(一元谓词上的序)。然后，她在双层模型中综合考察了所有在上面两个模型中讨论过的动态算子，证明了一些对应定理：在可能世界上的偏好动态变化正好对应在优先序上的某个动态算子，反之亦然；另一方面，也证明了一些否定性的结果，表明并非所有的算子都能找到对应。

从数理逻辑的角度研究博弈由来已久。一个问题是，带有随机行动的博弈对应什么样的逻辑？在2013年的工作中，鞠实儿和文学锋将布林诺夫(A.Blinov)提出的带随机行动的语义博弈与布莱米(S.Blamey)提出的部分逻辑(partial logic)关联起来，为部分逻辑提供了若干博弈语义，通过把桑杜(G.Sandu)等人提出的IF命题逻辑等价地翻译为部分逻辑，他们间接地证明了：在IF命题逻辑对应的语义博弈中，不完美信息并不是必要的，而是可以由随机行动代替。他们还指出，IF谓词逻辑的某些片段可以翻译为一阶部分逻辑，从而说明，IF逻辑中某些量词的独立性是由量词次序的不确定性造成的。此外，他们还考察了在更一般的逻辑与博弈背景下，如何将带随机行动的博弈扩展到其他种类的逻辑博弈，以及在博弈逻辑中引入表达随机行动算子的可能。2018年，文学锋研究了“判断聚合理论中的不可能性结果究竟适用于哪些逻辑”这一问题。尽管迪特里希(F.Dietrich)和蒙欣(P.Mongin)给出的判断聚合理论的一般逻辑模型已经具有较大的普遍性，但却将所有非单调逻辑均排除在外了。他论证了在判断聚合中使用非单调逻辑的必要性，区分了判断聚合中非单调逻辑的两种使用：解决不一致性和知识表达。论文证明了判断聚合理论的基本结果可以推广到非单调逻辑的情况。已有文献在证明这些结果时，通常在不同假定下给出不同证明。文学锋将两个不同假定下的证明融合为一个统一的证明，并澄清了证明中所需要的逻辑假定；作为副产品，他还证明了一类非单调逻辑的近似表征结果。[※注]

有鉴于公共知识在动态认知逻辑框架中的研究已较为完善，王轶等人在2013年的论文《带分布式知识的公开宣告逻辑：表达力、完全性和复杂性》关注与之相对的分布式知识的动态认知刻画：首先对比公开宣告逻辑(最简单的动态认知逻辑之一)中增加公共知识和/或分布式知识算子所得逻辑的相对表达能力，然后探讨这些逻辑的公理系统，特别是完全性证明；他们采用“伪模型—树展开—折叠”方法，将涉及关系交运算(分布式知识即是一例)的公理系统的完全性证明提炼为验证语言中的有关算子是否对“跨类型互模拟”封闭；证明了同时带有公共知识和分布式知识的动态和静态认知逻辑的有效性检测问题都是EXPTIME完全的。2016年，王轶出版《混合空间逻辑》，从混合逻辑(Hybrid Logic)在模态逻辑基础上所引入的“混合均衡观”和可能世界语义学中“视野缩小意味着知识增加”的约定出发，厘清由模态逻辑扩充为混合逻辑、由克里普克语义学切换至空间语义学后的比较重要的转变和相关的语形、语义、元性质(特别是模型论)结果，并以认知推理为导向将其拓展至混合空间逻辑的研究。混合逻辑、拓扑逻辑和子集空间逻辑是由哲学逻辑前沿研究所促成的三个分支学科，将三者结合起来的探索可以结合应用领域的特点和需求，引发对新理论和方法的探究，“混合空间逻辑”即是这一背景下的产物。[※注]

人们通过提供理由来证明知识。欣迪卡(J.Hintikka,1929—2015年)语义将知识刻画为真的信念。证明逻辑补充了柏拉图将知识描述为被证明为真的信念所缺失的第三个要素。证明逻辑(Justification Logics)的思想源于20世纪30年代哥德尔关于直觉主义逻辑的算术语义研究，阿逖莫夫(S.Artëmov)在90年代独立提出证明的逻辑(Logic of Proofs)，逐渐发展成前者，是可证性逻辑的当代形式。证明逻辑在如下意义上是一种“显式”模态逻辑：公式A是模态定理，当且仅当在证明逻辑中有一条称为A的“实现”的定理，是通过用(证明)词项置换A中的模态词的出现而得到的，这些词项的结构显式地解释了它们的可作证据的内容。从这种意义上说，证明逻辑把证明“内部化”。源于20世纪50年代普莱尔工作的混合逻辑则是把可能世界语义“内部化”。菲廷(M.Fitting)把二者结合在一起，于2010年提出混合的证明逻辑方向，刘新文及其学生在2015年解决了他所提出的极小系统问题。在证明逻辑中，词项代表公式(所表达的命题)的证明，常项作为一类原子公式，代表公理的证明；已经证明，为了实现一些模态定理，有必要使用自指常项(自指常项表示的是包含这个常项本身的出现的公理的证明)。2017年，俞珺华研究了模态逻辑的非自指片段，并且证明了：(1)这个片段一般不对分离规则封闭；(2)当从一个较小的模态逻辑到一个较大的模态逻辑时，该片段通常不是“保守的”。[※注]

知识逻辑(Epistemic Logic)是哲学逻辑的一个重要分支，传统上研究用“知道如是”(knowing that)表达的知识的推理规则。然而，在日常生活中我们还会使用诸如“知道是否”(knowing whether)、“知道如何”(knowing how)、“知道为何”(knowing why)、“知道是什么”(knowing what)等表达式来表述知识(统称knowwh)。在知识逻辑发展的初期，欣迪卡曾提出用一阶模态逻辑来处理这样的表达式。例如，“A知道谁杀了B”可以写成“存在一个人x,A知道x杀了B”。量词和模态词在这里的顺序非常重要，如果写成“A知道存在一个人x,x杀了B”，意思就完全不一样了，这恰好体现了哲学中从物(de re)与从言(de dicto)的区分。然而，由于一阶模态逻辑的各种哲学及技术问题，后来的知识逻辑的文献中鲜有讨论这样的知识表达式，甚至在2015出版的《知识逻辑手册》[※注]中也几乎没有任何关于一阶知识逻辑或者know-wh的讨论。2015年前后，王彦晶提出一条处理know-wh的逻辑的系统性新进路[※注]：将量词与模态词打包定义为新的know-wh模态词，例如直接引入“知道如何”这样的模态词(“知道如何实现p”的语义是存在一个计划x主体知道这个计划x可以保证p)[※注]，而不使用整个的一阶模态逻辑的语言。这样做的好处是可以在技术上避免一阶模态逻辑整体上的一些问题，表达更接近自然语言，可以得到类似传统知识逻辑的比较直观的公理。更有意思的是，这样的打包会限制量词的出现，帮助我们得到一系列一阶模态逻辑的新的可判定片段[※注]。这种打包量词与模态词的思路可以让知识逻辑的领域更加丰富，得到一系列直观的关于know-wh的逻辑系统，启发哲学及语言学上的相关讨论，在人工智能的领域中推动关于各种知识的表示与推理的应用。当然，这种做法也带来了很多技术方面的挑战，比如所有这些逻辑都是非正规的模态逻辑，逻辑语言弱而模型丰富，公理化及完全性证明比较困难。王彦晶及其学生与合作者系统性地研究了“知道是否”“知道是什么”“知道如何”“知道为何”以及“知道是谁”等的逻辑，开发出一系列处理相应技术问题的新方法，同时也发现了这些逻辑从技术上与之前哲学逻辑文献中已有逻辑的种种联系，开拓了知识逻辑的新方向。

在哲学逻辑领域，对于公理化、可判定性等基本问题的研究多针对特定的逻辑系统，很少有适用于多个系统的一般性结论。2015年，张炎和李楷发表的论文从逻辑类的角度出发，研究基于非决定离散时态逻辑的多维模态逻辑类的可判定性问题，试图改变这个现状。这类逻辑的语言除了包含常见的时态算子外，还有多个一般模态算子，其意义依赖于所对应的框架条件。他们首先给出了定义这类逻辑的语义结构——通用框架(generic frames)，这是一种以奥卡姆框架为核心的、多维的克里普克框架，一般性的模态算子通过在其上添加若干个二元关系来解释。他们从语法上定义了两集一阶框架语言中的语句，并且证明：对任意的通用框架类 C，如果C可被上述集合中的语句定义，那么 C 决定的多维模态逻辑是可判定的。这个结论可以应用到包含时态的多种哲学逻辑上，论文展示了一个这样的应用，并得出多个时态认知 stit 逻辑的可判定性。1969年，拉宾(M.Rabin)证明了S ωS 是可判定的，其中 S ωS 是含ω个后继函数的带根 N 型(N 型是指树中每个极大枝都与自然数上的序同构)树——拉宾树的一元二阶理论。因为一元二阶语言强大的表达力和树结构的普遍性，拉宾定理在模态逻辑以及哲学逻辑界有着广泛的应用；拉宾树中每个极大枝都与自然数上的序同构，并要求存在最小元树根。2017年，张炎通过归约方法证明：Z-型拉宾树的一元二阶理论是可判定的；Z-型拉宾树是拉宾树的一种变体，它们与拉宾树的主要区别在于不要求树根的存在，而只限制其中的极大枝与整数上的序同构。[※注]

2018年，刘奋荣与范·本特姆(J.van Benthem)合作撰写的《道义逻辑与改变偏好》[※注]发表在第二版《哲学逻辑手册》第18卷。同一年，琚凤魁发表《作为道义逻辑的S5》，构造了一个简单的动态道义逻辑SimDDL，用来形式化条件义务、禁令以及允许改变我们的义务的方式。SimDDL有两个部分，静态部分是模态逻辑S5的一个变种S5 c，可以定义两种类型的义务：理想义务和实际义务。它的动态部分包含三个动态算子，能够解决一些道义悖论。这三个动态算子并不增加SimDDL的表达力，因此，它的完全性可以归约为S5 c的完全性。[※注]

量子逻辑在国内哲学工作者中从业者很少，钟盛阳近年来发表了一些研究成果。量子系统的(纯)状态之间的非正交关系是自返和对称的，并且模态逻辑系统KTB相对于自返对称框架所组成的框架类是可靠和强完全的。在2018年发表的论文《论量子状态之间的非正交关系的模态逻辑》中，钟盛阳考虑非正交性关系的两个性质——分离性和叠加性，给出相对于满足自返性、对称性和分离性的框架所组成的框架类可靠且强完全的模态逻辑系统，也给出相对于满足自返性、对称性、分离性和叠加性的框架所组成的框架类可靠且强完全的模态逻辑系统，还证明了这两个模态逻辑都是可判定的。此外，在论文《克里普克框架与射影几何之间的对应关系》中，钟盛阳考察了一些在数学和量子理论中广泛使用的正交几何，即通过三元共线关系定义并配备二元正交关系的射影几何，证明它们对应于使用二元关系定义并满足一些条件的克里普克框架。确切地说是定义了四种特殊的克里普克框架，即几何框架、不可化约的几何框架、完备的几何框架和量子克里普克框架，证明了它们分别对应于纯的正交几何(或者等价地，具有纯的极性的射影几何)、不可化约的纯的正交几何、希尔伯特几何和不可化约的希尔伯特几何。[※注]

2018年，马明辉及其学生运用矢列演算研究了模态逻辑的全局后承关系：正规模态逻辑的所有全局矢列演算都容许全局切割消除，这个性质被用来证明K4上的任意正规模态逻辑从局部后承理论到全局后承理论的可判定性和插值性质的保持定理。同一年，马明辉在皮尔士逻辑图的深度演算系统方向建立起布尔代数以及分配格等逻辑代数的逻辑图演算系统。[※注]在2014年的论文《弗雷格式量化逻辑》中，克里普克将弗雷格的“句子作为专名”这一思想进行了推广和研究，提出了一个弗雷格式量化逻辑FQ;2016年，马明辉和刘新文在论文《论克里普克的弗雷格式量化逻辑》中指出FQ不是对一阶逻辑的重新表述，问题出在条件句算子的解释。为了把FQ中的一些有效项公理化，基于克里普克提出的句法和语义，马明辉和林渊雷在2019年的论文中提出了一个可靠和完全的三值弗雷格式量化逻辑FQsup3，这个三值逻辑不同于克里尼(S.Kleene)和卢卡西维茨的三值逻辑，它是可判定的。[※注]同一年，马明辉和林渊雷还发表了贝尔纳普和邓恩(J.M.Dunn)四值逻辑的弱化系统，研究了其矢列演算系统和关系语义学。[※注]

第四节 结语

逻辑学和数学一样同属于基础学科。70年来，我国几代哲学工作者在哲学逻辑的基础和前沿领域发表了大量研究成果，不仅为我国哲学领域的逻辑学科赢得了国际学术地位，而且对我国哲学学科的整体发展起到了积极的推动作用。如果数理逻辑和哲学逻辑等现代逻辑基础课程可以在更大范围内普及，以此为基础的研究就会在更大范围内得到开展和提高，从而更加有利于促进逻辑学科本身和哲学学科的发展，更加有利于加快构建中国特色哲学社会科学学科体系、学术体系、话语体系。

致谢：在本章的写作过程中，中国社会科学院哲学研究所领导给予了高度重视和宏观指导，北京大学宋文坚教授、北京师范大学宋文淦教授、中国社会科学院哲学研究所张尚水研究员和张家龙研究员等学界前辈给予了具体指导，许多逻辑学一线工作者提供了大量帮助，特此致谢！